MODELING OF HARMONIC GENERATION
AND SHOCK FORMATION
IN NONLINEAR SURFACE ACOUSTIC WAVES
IN SEVERAL REAL CRYSTALS
R. E. Kumon and M. F. Hamilton
Department of Mechanical Engineering
The University of Texas at Austin
Yu. A. Il'inskii and E. A. Zabolotskaya
MacroSonix Corporation
Richmond, Virginia
Paper 1aPA2
134th Meeting of the Acoustical Society of America
San Diego, California
1-5 December 1997
J. Acoust. Soc. Am. 102, 3064 (1997)
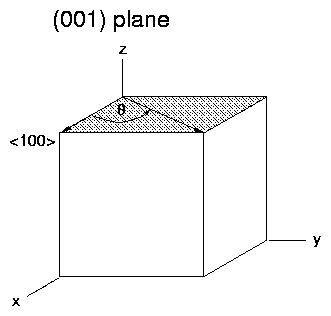
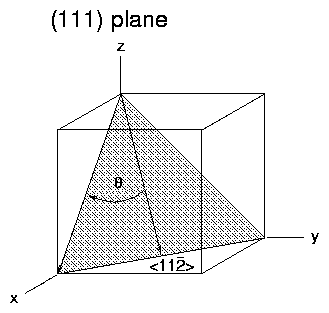
ANISOTROPY AND CUBIC CRYSTALS
Stress-strain relation:
|
| |
|
|
| |
|
|
Second Order Elastic (SOE) constants |
| |
|
|
Third Order Elastic (TOE) constants |
|
| |
| |
Cubic crystals:
|
Parameters | Cubic Crystal | Isotropic
|
SOE | 3 independent
| 2 independent
|
TOE | 6 independent
| 3 independent
|
Anisotropy Ratio |
h = 2c2323/(c1111-c1122) |
h = 1 | | | |
Specific Examples:
|
Crystal | Type | Anisotropy Ratio h
|
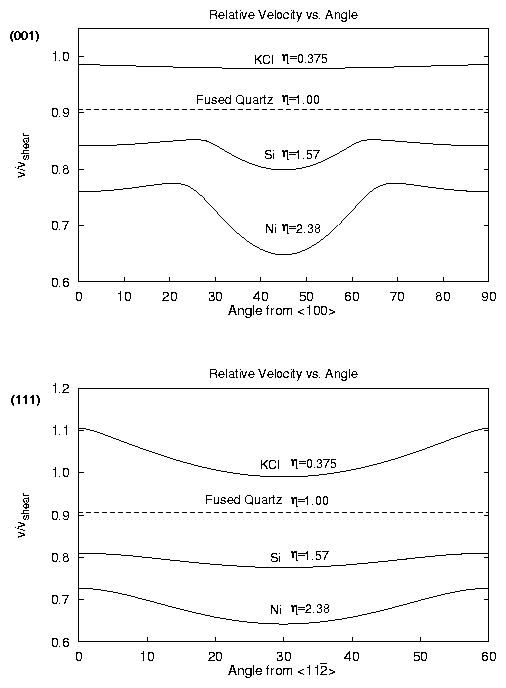
KCl | Face-centered cubic | 0.375
|
Ni | Face-centered cubic | 2.38
|
Si | Diamond cubic | 1.57 | | | |
Cubic Crystal Types:
Typical Planes for Crystal Cuts:
THEORY
Approach:
- Hamiltonian formalism (Hamilton, Il'inskii, Zabolotskaya, 1996)
Velocity waveforms in solid:
|
| |
|
|
|
|
¥
å
n = -¥
|
vn(x) uni(z) ein(k0x-w0t) |
| |
|
|
|
3
å
s = 1
|
b(s)i eink0l(s)3z |
|
| |
| |
Coupled spectral evolution equations:
|
|
|
|
dvn
dx
|
+an vn = |
w0 n2
2rc4
|
|
æ
è
|
2 |
¥
å
m = n+1
|
R*m-n,nvmv*m-n - |
n-1
å
m = 1
|
Rm,n-mvmvn-m |
ö
ø
|
|
|
| |
| |
Solution Procedure:
- Numerically solve linear problem for eigenvalues, eigenvectors, and small-signal wave speed c.
- Construct nonlinearity matrix Rmn.
- Numerically integrate spectral evolution equations using a 4th order Runge-Kutta routine
( ~ 200 harmonics).
WAVE SPEED VARIATION
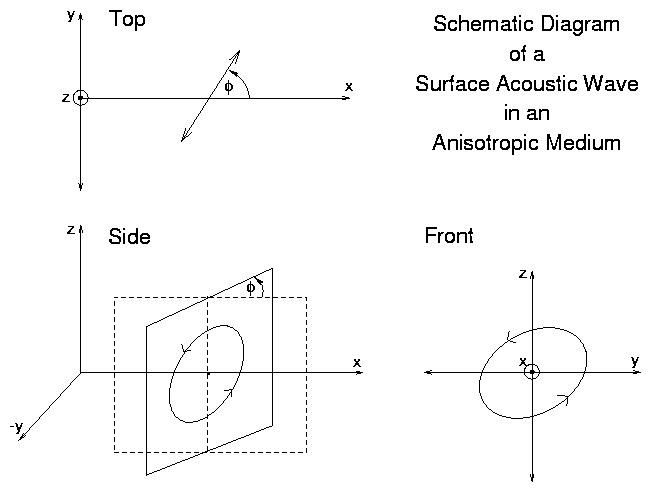
SCHEMATIC DIAGRAM
WAVEFORM DISTORTION: CRYSTALS
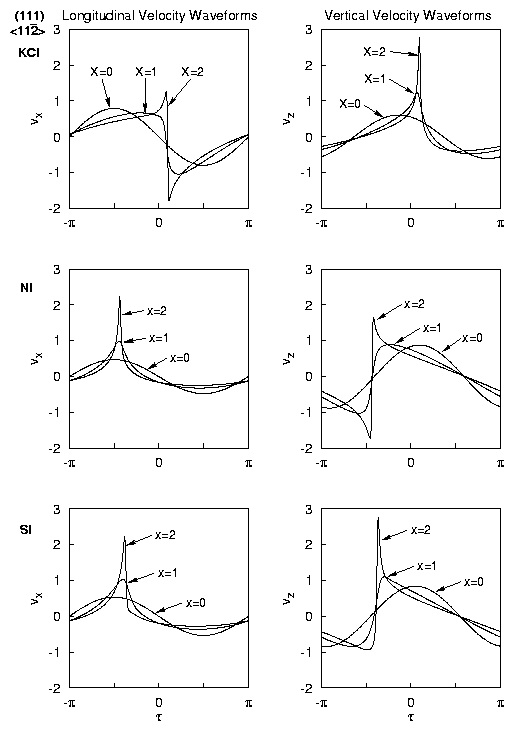
WAVEFORM DISTORTION: DIRECTIONS

ATYPICAL ENERGY TRAPPING
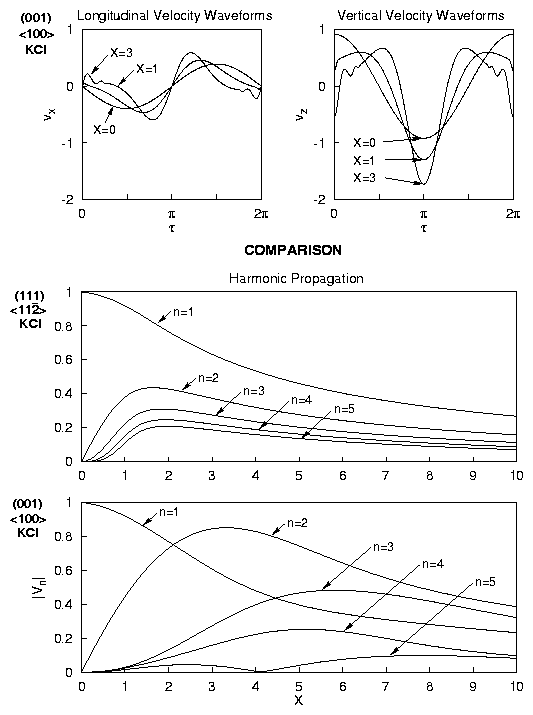
Truncated system of evolution equations (no dissipation):
|
|
dv1
dx
|
= |
w0
rc4
|
R11* v2 v1* , |
dv2
dx
|
= - |
2w0
rc4
|
R11 v12 |
|
Boundary conditions:
|
v1 = v0 , v2 = 0 at x = 0 |
|
Analytical solution:
|
|
|v1|
v0
|
= sech |
æ
ç
è
|
|
1
2Ö2
|
|
x
x0
|
|
ö
÷
ø
|
, |
|v2|
v0
|
= Ö2 tanh |
æ
ç
è
|
|
1
2Ö2
|
|
x
x0
|
|
ö
÷
ø
|
|
|
Graphical Comparison of Numerical & Analytical Results:
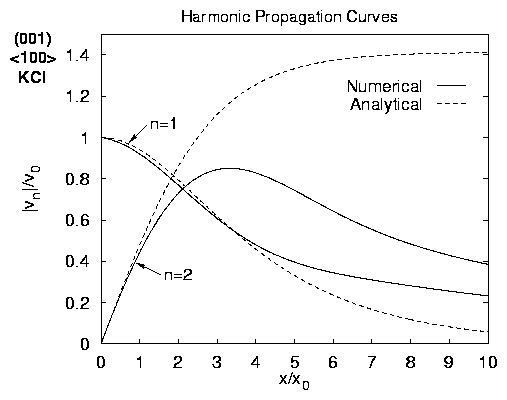
CONCLUSION & FUTURE WORK
Results:
- Cubic crystal waveforms exhibit:
- Asymmetric distortion
- Shocks with cusped spikes
- Phase shift of waveforms as function of direction
- Prediction of atypical energy trapping in
lowest harmonics in a nondispersive medium:
- KCl for (001) plane in á100ñ direction
- Approximate analytical solution close to source
Future work:
- Relationship between nonlinearity matrix and waveforms
- Analytical expression for shock formation distance
- Pulsed waveform modeling and experimental data comparison
- Investigation of other crystals besides cubic
File translated from TEX by TTH,
version 0.99 with some minor editing by Ronald Kumon.